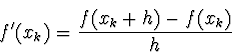 |
(5.51) |
als Näherung für die partiellen Ableitungen. (Für uxxx drei mal interieren)
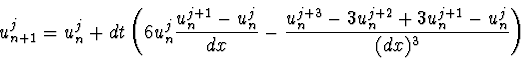 |
(5.52) |
Betrachte zunächst eine einfache Diskretisierung:
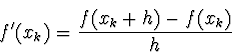 |
(5.51) |
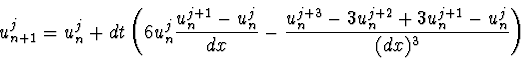 |
(5.52) |
Problem: Schlechte Lösung, da Solitonen nicht stabil sind, wenn sie sich durchdringen, d.h. schon nach wenigen Zeitschritten ''explodiert'' die Lösung.
Fehlerursachen
Analog zum Vorgehen beim Numerov-Verfahren kann man die
erste Ableitung besser Darstellen. Betrachte dazu die Taylorreihe
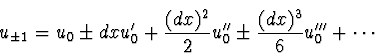 |
(5.53) |
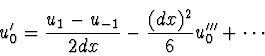 |
(5.54) |
Man verwende hierzu statt
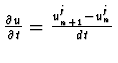 besser den Mittelwert, den man
durch die Substitution
besser den Mittelwert, den man
durch die Substitution
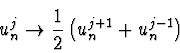 |
(5.55) |
Unterschied zur genaueren Ableitung wie bei 1.???
Definition: Courant-Bedingung
Störungen bleiben nur dann stabil, wenn der Zeitschritt dt kleiner
als der Ausbreitungsschritt ![]() ist.
ist.
Beachte: Nach der symmetrischen Diskretisierung enthält die Gleichung nun drei Zeitschritte, d. h. für die Berechnung der Zukunft (n+1) muß man Gegenwart n und Vergangenheit n-1 kennen. der erste Schritt (hier ist nur die Gegenwart bekannt!) muß nach der einfachen Formel erfolgen, die weiteren dann mit den beiden symmetrischen Diskretisierungen
Beachte: Man kann den Fehler der numerischen Approximation durch
verkleinern der Schrittweite reduzieren. Dabei wächst der Aufwand für
die Berechnung in x-Richtung mit ![]() .
Aus Stabilitätsgründen
muß aber dt
.
Aus Stabilitätsgründen
muß aber dt
![]() verkleinert werden!
verkleinert werden!