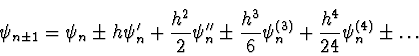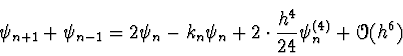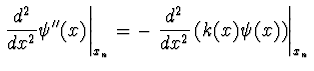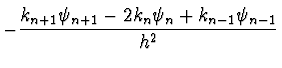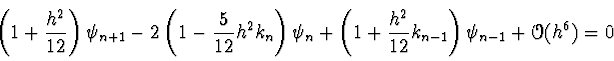5.4.3 Numerov-Verfahren

(s. z.B. Stoer II, 7.4)

Ziel: Größere Genauigkeit bei einfacherem Verfahren

Prinzip: Diskretisierung des Intervalls und Näherung der Differentiale durch geeignete Differenzenquotienten

Beachte: Problemabhänig, funktioniert also nicht allgemein! (Im Unterschied zum Runge-Kutta-Verfahren) Anwendung auf Gleichungen der Form:

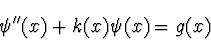$$\psi''(x) + k(x) \psi(x) = g(x)$$ (5.41)

wobei hier k(x) = 2(E-V(x)) und g(x) = 0

Voraussetzungen:

• k(x) stetig
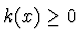• $k(x) \geq 0$ für $x \in [a,b]$

Damit kann man zeigen, daß eine eindeutige Lösung existiert. Für die Anwendung hier ist g(x) = 0, die Gleichung selbst mit -1 multipliziert.

Verfahren:

• Teile das Intervall [a,b] in n+1 äquidistante Teile:
  

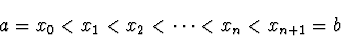  $$a = x_0 < x_1 < x_2 < \cdots < x_n < x_{n+1} = b$$ (5.42)

  
  
  wobei 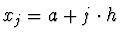$x_j = a+ j \cdot h$ mit $h := {b-a \over n+1}$

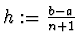
• Definition: $\psi_j = \psi(x_j)$ $\psi_i'' = \psi''(x_i)$
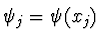
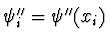
• Betrachte die Taylorentwicklung
  

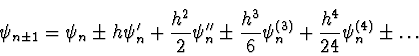  $$\psi_{n \pm 1} = \psi_n \pm h \psi_n' + {h^2 \over 2} \psi_... ...ver 6} \psi_n^{(3)} + {h^4 \over 24} \psi_n^{(4)} \pm \ldots$$ (5.43)

  
  

• Betrachte nun $\psi_{n+1} + \psi(n-1)$:
  
  

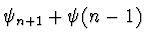• Neue Taylorreihe nach dieser Substitution:
  

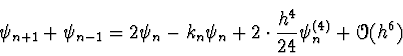  $$\psi_{n+1} + \psi_{n-1} = 2 \psi_n - k_n \psi_n + 2 \cdot {h^4 \over 24} \psi_n^{(4)} + \Order(h^6)$$ (5.44)

  
  

• Ersetze damit die 4. Ableitung durch die diskretisierte zweite (durch Auflösen nach $\psi_n^{(4)}$):
  

  $$\psi_n^{(4)} \left. {d^2 \over dx^2} \psi''(x) \right\vert _{x_n} = - \left. {d^2 \over dx^2} \left( k(x) \psi(x) \right) \right\vert _{x_n}$$ =

  $$- {k_{n+1} \psi_{n+1} - 2 k_n \psi_n + k_{n-1} \psi_{n-1} \over h^2 }$$ = (5.45)

  $$\mbox{da mit der Taylorreihe gilt}$$

  $$h^2 \psi_n'' \psi_{n+1} + \psi_{n-1} - 2 \psi_n$$ = (5.46)

  
  

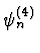• Einsetzen in die Taylorreihe ergibt
  

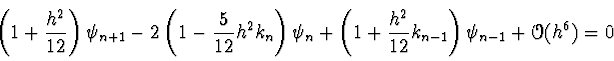  $$\left( 1 + {h^2 \over 12} \right) \psi_{n+1} - 2 \left( 1 ... ...+ {h^2 \over 12} k_{n-1}\right) \psi_{n-1} + \Order(h^6) = 0$$ (5.47)

  
  

• Aus zwei benachbarten Startwerten kann man sämtliche 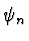$\psi_n$-Werte berechnen.

Anpassungen an das Problem:

• Intervalle:
  • gerade Wellenfunktion: $x_n = \left( n-\einhalb \right) h$
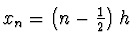
  • ungerade Wellenfunktion: x_n = n h
• Startwerte: Wegen der Symmetrie des Potentials
  • gerade Wellenfunktion: $\psi_0 = \psi_1 \neq 0$
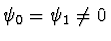
  • ungerade Wellenfunktion: $\psi_0 = 0, \psi_1 \neq 0$
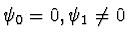
  Wobei 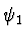$\psi_1$ beliebig ist, da er nicht den Energieeigenwert, sondern wegen der Linearität der Schrödingergleichung nur die Normierung ändert
• Programmierung: Berechne Konstanten nicht innerhalb der Scheife jedes mal neu, sondern einmal am Anfang der Prozedur um CPU-Zeit zu sparen!

Vorteil dieser Methode gegen die Näherung durch Diagonaliserung einer endlichen Untermatrix: Man erhält eine obere und untere Schranke, und kann die Genauigkeit über Halbierung der Schrittweite prüfen.