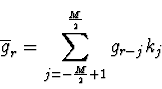 |
(2.40) |
Prinzip: Mitteln des Wertes an einem Punkt durch gewichtetes Mitteln der Daten um einen Punkt herum. Zur Wichtung verwendet man eine Gaußglocke um unerwünschte neue Strukturen zu vermeiden, d. h. jeder Datenpunkt wird entsprechend seinem Abstand vom aktuellen Meßwert mit einer Gaußfunktion gewichtet.
Prinzip: Entspricht dem Falten der Meßfunktion g mit einer Gaußfunktion k.
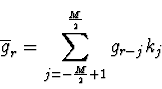 |
(2.40) |
Die Gaußglocke heißt auch
Gewichtsfunktion oder Kern. Dieser muß normiert
sein, d. h. bei Betrachtung diskreter Datenpunkte gilt
![]() .
.
Betrachtet wird die diskrete Folge gi = fi + ri, wobei fi die eigentlichen Funktionswerte, und ri das Rauschen darstellt. Die gemittelte Funktion wird als
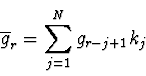 |
(2.41) |
wenn man lt. Kienzel die Glaußkurve symmetrisch so in das Intervall kj legt, daß das Maximum bei 1 liegt und die Intervalle bei 1 loslaufen.
Mit Hilfe der Fouriertransformierten kann man g's und k's schreiben als:
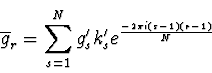 |
(2.42) |
da für die Faltung von Funktionen gilt:
| hr | = | 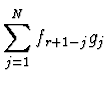 |
(2.43) |
| = | 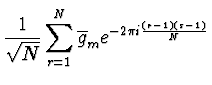 |
(2.44) | |
| gj | = | 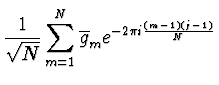 |
(2.45) |
| fr+1-j | = | 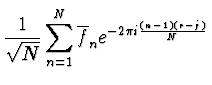 |
(2.46) |
| = | 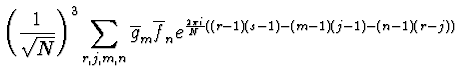 |
(2.47) | |
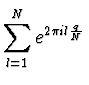 |
= | (2.48) |
Beachte
![]() womit sich ergibt:
womit sich ergibt:
| = | 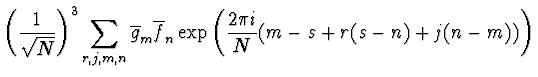 |
(2.49) | |
| = | 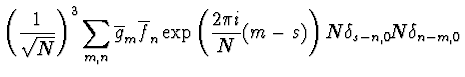 |
(2.50) | |
| = | 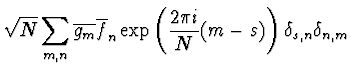 |
(2.51) | |
| = | 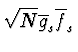 |
(2.52) |
Wichtige Punkte für die Glättung