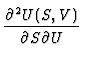



Next: 6.2 Enthalpie H
Up: 6. Thermodynamische Potentiale und
Previous: 6. Thermodynamische Potentiale und
Inhalt
Index
Fundamentalgleichung
dU = TdS - pdV + 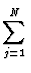 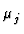 dNj dNj
|
(86) |
Da dU ein vollstndiges Differential ist, gilt:
dU = 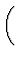 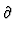 U U 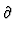 S S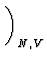 dS + dS + 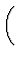 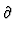 U U 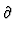 V V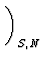 dV + dV + 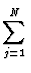 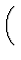 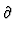 U U 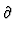 Nj Nj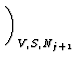 dNj dNj
|
(87) |
Das Differential hat die Form: ''intensive Variable x Differential
einer extensiven Variablen''. Das gilt nur fr dU!
Durch Vergleich findet man
| p(S, V) |
= |
- 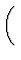 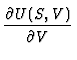
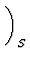 |
(88) |
| T(S, V) |
= |
- 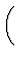 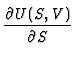
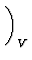 |
(89) |
Bestimmt man aus der zweiten Gleichung S = S(T, V) ergeben sich durch
Einsetzen die thermische bzw. kalorische Zustandsgleichung:
| p |
= |
p(S, V) = p(S(T, V), V) = p(V, T) |
(90) |
| U |
= |
U(S, V) = U(S(T, V), V) = U(V, T) |
(91) |
12cm
U(S, V) ist eine Funktion von extensiven Variablen,
aus der die intensiven Variablen als partielle Ableitungen
hervorgehen U(S, V) ist ein thermodynamisches
Potential. Die intensiven Variablen bezeichnet man auch als
verallgemeinterte Krfte, bei U(S, V) spricht man von einer
Fundamentalgleichung
Weiterhin gengt U(S, V) der Integrabilittsbedinung
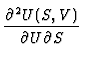 =
= 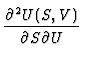
|
(92) |
(Satz von Schwarz), so daá man durch geeignetes Partielles
Ableiten die Maxwellrelationen erhlt:
Anwendung: Abgeschlossene Systeme
Der ''Teilchenzahlterm'' zieht sich bei allen Rechnungen mit,
die Maxwellrelationen bleiben aber unverndert (d.h. sie
gelten bei zustzlich konstanter Teilchenzahl). Im Folgenden wird
daher auf das mitschleifen des Teilchenzahlterms verzichtet.




Next: 6.2 Enthalpie H
Up: 6. Thermodynamische Potentiale und
Previous: 6. Thermodynamische Potentiale und
Inhalt
Index
Alexander Wagner
2000-04-15
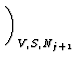 dNj
dNj
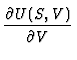
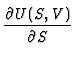
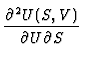 =
=