Nsc(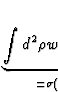 ( ( |
(29) |
Der Wirkungsquerschnitt ist definiert durch die Anzahl der Teilchen, die bei einem Streuprozess in einen bestimmten Raumwinkelbereich gestreut werden:
Nsc(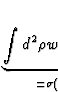 ( ( |
(29) |
Quantenmechanisch gilt nun fr die Wahrscheinlichkeit ein gestreutes
Teilchen mit Impuls ![]() im Raumwinkelelement d
im Raumwinkelelement d![]() zu finden
zu finden
|
w(d |
(30) |
Damit ergibt sich, wenn ninc die konstante Dichte der
einfallenden Teilchen (Wellenpakete) ist fr die Anzahl der in das
Raumwinkelelement d![]() gestreuten Teilchen
gestreuten Teilchen
|
Nsc(d |
(31) |
Die hier angenommenen Bedingungen sind meist gut erfllt. Ein bekanntes Beispiel wo sie nicht gelten ist das Davisson-Germer-Experiment. Hier werden Elektronen senkrecht und monoenergetisch auf eine Nickeloberflche geschossen. Man findet im Streuwinkel ein ausgeprgtes Maximum bei 0und ein weiteres bei 50. Das 50-Maximum lát sich aus der Streutheorie nicht erklren, es resultiert aus konstruktiver Interferenz der Elektronenwellen.
Fr die Berechnung des quantenmechanischen Wirkungsquerschnitts findet
man nun :
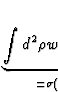 (d (d |
= | 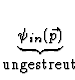 ) ) |
(32) |
w(d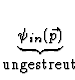 ) ) |
= | d |
(33) |
| = | 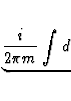 |
(34) | |
| = | 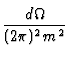 |
(35) | |
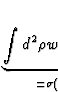 (d (d |
= | ||
| x |
|||
| x |
(36) |
Die erste Vereinfachung erhlt man durch Einsetzen von
| = | (2 |
(37) | |
| = | 2m |
(38) | |
| = | (39) |
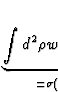 (d (d |
= | d |
(40) |
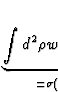 (d (d |
= | d |
(41) |
7cm
|
|
(42) |
Die bei der Herleitung ntige Bedinung, daá
f (![]()
![]()
![]() ) scharf genug ist geht in der Rechnung da ein, wo
f (
) scharf genug ist geht in der Rechnung da ein, wo
f (![]()
![]()
![]() ) aus dem Integral gezogen wird. Man
findet, daá diese Funktion in engem Zusammenhang mit der
Fouriertransformierten des Streupotentials steht. Praktisch bedeutet
die Bedinung, daá die Wellenfunktion im Ortsraum breit gegen das
Streupotential sein muá (quasi einlaufende ebene Wellenfront), da sie
dann im Impulsraum schmal ist.
) aus dem Integral gezogen wird. Man
findet, daá diese Funktion in engem Zusammenhang mit der
Fouriertransformierten des Streupotentials steht. Praktisch bedeutet
die Bedinung, daá die Wellenfunktion im Ortsraum breit gegen das
Streupotential sein muá (quasi einlaufende ebene Wellenfront), da sie
dann im Impulsraum schmal ist.