


Next: 3.2 On-Shell T-Matrix und
Up: 3. Wirkungsquerschnitte und S-Matrix
Previous: 3. Wirkungsquerschnitte und S-Matrix
Index
Der Streuoperator S erhlt die Energie. Da S die einlaufenden
asymptotischen Zustnde auf die auslaufenden asymptotischen Zustnde
abbildet bedeutet das, daá S mit H0 (= kinetische
Energie) kommutiert, nicht mit H. Fr die Streuoperatoren gilt
H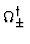 =
= 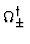 H0 H0
|
(21) |
Da die Mølleroperatoren isometrisch sind ist dies gleichbedeutend
mit
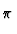 H H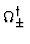 = H0
= H0
|
(22) |
Daran sieht man ebenfalls, daá die Mølleroperatoren i.A. nicht
unitr sein knnen, da sonst H und H0 das selbe
Spektrum htten, also z. B. H keine gebundenen Zustnde
haben drfte (da ja H0 keine hat). Anders herum knnen die
Mølleroperatoren nur dann unitr sein, wenn es keine gebundenen
Zustnde gibt.
S kommutiert mit H0:
SH0 = 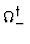 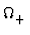 H0 = H0 = 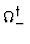 H H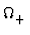 = H0
= H0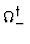 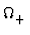 = H0S
= H0S
|
(23) |
Um die Vertauschbarkeit von S mit H0 ausnutzen zu knnen
entwickelt man in eine Basis aus Eigenvektoren. Da
aber H0 der Hamiltonoperator eines freien Teilchens ist, gibt es
keine echten Eigenvektoren und man muá mit den Impulsen arbeiten. Die
Wellenfunktion zu den Impulseigenvektoren sind ebene Wellen
wobei man 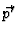 auf die dreidimensionale Deltafunktion
normiert, d. h.
auf die dreidimensionale Deltafunktion
normiert, d. h.
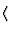
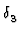 |
|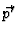
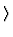 =
= 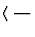
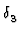 -
-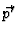 . Damit folgt fr das
S-Matrixelement in Impulsdarstellung
. Damit folgt fr das
S-Matrixelement in Impulsdarstellung
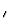
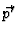
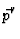 S
S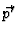 , was oft schlicht als die
S-Matrix bezeichnet wird. Der Vorteil der ebenen Wellen ist,
daá sie eine brauchbare Basis fr die Entwicklung der wahren
Eigenzustnde darstellen:
, was oft schlicht als die
S-Matrix bezeichnet wird. Der Vorteil der ebenen Wellen ist,
daá sie eine brauchbare Basis fr die Entwicklung der wahren
Eigenzustnde darstellen:
Damit ergibt sich die Energieerhaltung im Impulsraum zu
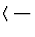 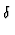 S S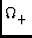  =
=  (Ep' - Ep) x (Rest) (Ep' - Ep) x (Rest)
|
(26) |



Next: 3.2 On-Shell T-Matrix und
Up: 3. Wirkungsquerschnitte und S-Matrix
Previous: 3. Wirkungsquerschnitte und S-Matrix
Index
Alexander Wagner
2000-04-15