Eigenfunktionen des Drehimpulsoperators ![]() und
und ![]() in
der Quantenmechanik 4.4
in
der Quantenmechanik 4.4
|
fn(x) = Pn(x) mit 0 |
(4.26) |
|
P0(x) = 1 P1(x) = x P2(x) = |
(4.27) |
allgemein:
|
Pn(x) = |
(4.28) |
P2n + 1(0) = 0 P2n(0) = (- 1)n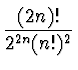 Pn(
Pn( |
(4.29) |
Rekursionsformel:
| (n + 1)Pn + 1(x) = (2n + 1)xPn(x) - nPn - 1(x) | (4.30) |
|
((1 - x2) |
(4.31) |
(1 - x2)Pn'(x) = n(Pn - 1(x) - xPn(x)) = 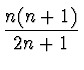 (Pn - 1(x) - Pn + 1(x)) (Pn - 1(x) - Pn + 1(x))
|
(4.32) |
Pl(cos(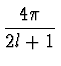 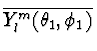 Ylm( Ylm( |
(4.33) |
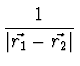 =
= 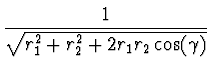 =
= |
(4.34) |