|
fn = Hn(x) mit 0 |
(4.5) |
Energieeigenfunktionen des harmonischen Oszillators in der Quantenmechanik4.1
|
fn = Hn(x) mit 0 |
(4.5) |
Nn2 = 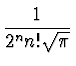 a = - a = - |
(4.6) |
| H0(x) = 1 H1(x) = 2x H2(x) = 4x2 - 2 H3(x) = 8x3 - 12x | (4.7) |
allgemein:
|
Hn(x) = (- 1)nex2 |
(4.8) |
H2n + 1(0) = 0 H2n(0) = 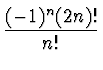
|
(4.9) |
Rekursionsformel zur Berechnung:
| Hn + 1(x) = 2xHn(x) - 2nHn - 1(x) | (4.10) |
|
|
(4.11) |