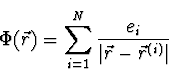 |
(2.57) |
Verwendung z. B. in der klassischen Elektrodynamik zur Beschreibung komplizierter Felder von Ladungsverteilungen.
Potential
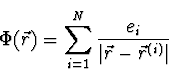 |
(2.57) |
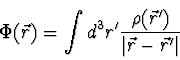 |
(2.58) |
Das elektrische Feld ist durch den Gradienten bestimmt
(
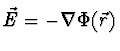 )
)
Man kann nun
![]() nach
Legendre-Polynomen oder Kugelfälchenfunktionen
entwickeln. 2.1 Hierzu betrachtet man die Differenz der beiden Ortsvektoren in
Kugelkoordinaten. Man kann dann mit dem Cosinussatz für
allgemeine Dreiecke schreiben:
nach
Legendre-Polynomen oder Kugelfälchenfunktionen
entwickeln. 2.1 Hierzu betrachtet man die Differenz der beiden Ortsvektoren in
Kugelkoordinaten. Man kann dann mit dem Cosinussatz für
allgemeine Dreiecke schreiben:
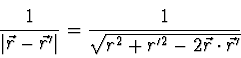 |
(2.59) |
Womit der Abstand
![]() eine Funktion der
Vektorbeträge und des Zwischenwinkels wird Entwicklung nach
Kugelflächenfunktionen ist möglich und es ergibt sich
eine Funktion der
Vektorbeträge und des Zwischenwinkels wird Entwicklung nach
Kugelflächenfunktionen ist möglich und es ergibt sich
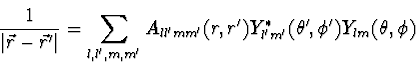 |
(2.60) |
Wendet man auf beide Seiten der Gleichung den
Laplace-Operator ![]() an, so findet man nach einiger
Rechnung unter Verwendung der Eigenschaften der
Kugelflächenfunktionen schließlich die allgemeine
Entwicklung
an, so findet man nach einiger
Rechnung unter Verwendung der Eigenschaften der
Kugelflächenfunktionen schließlich die allgemeine
Entwicklung
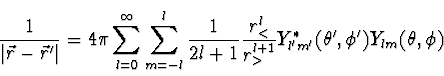 |
(2.61) |
Eingesetzt in das Potential ![]() ergibt sich die allgemeine
Multipolentwicklung. Als Multipolmoment bezeichnet
man
ergibt sich die allgemeine
Multipolentwicklung. Als Multipolmoment bezeichnet
man
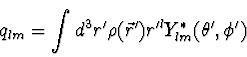 |
(2.62) |
Für eine Entwicklung bis zum Quadrupolmoment findet man also
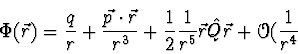 |
(2.63) |
--