| H2' = |
Substitutions | (170) | |
mit: 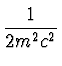 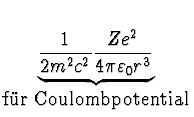 |
(171) |
Da L2 nicht auf r operiert kommutiet es mit allen Komponenten von L und auch mit H2', H2' verbindet also keine Zustnde mit verschiednen Drehimpulsquantenzahlen l. Man muá zur Lsung also eine 2(2l + 1) x 2(2l + 1)-Matrix diagonalisieren. Zur Vereinfachung benutzt man eine Darstellung der Wellenfunktionen in einer Basis in der L . S bereits diagonal ist.
![]() Einfhrung des Gesamtdrehimpulses
Einfhrung des Gesamtdrehimpulses
| J = L + S | Gesamtdrehimpuls | (172) | |
| J2 = L2 + S2 + 2L . S | und daraus | (173) | |
| L . S = |
(174) | ||
| mit den Eigenwerten: | (175) | ||
| J2 |
(176) | ||
| L2 |
(177) | ||
| S2 |
(178) | ||
| m |
(179) | ||
| (180) | |||
| j = l |
l |
(181) | |
| j = |
l = 0 | (182) |
In der neuen Basis ist die Strung bereits diagonal, die zugehrigen Wellenfunktionen ergben sich mit Hilfe der Clebsch-Gordon-Koeffizienten zu
| nlsjmj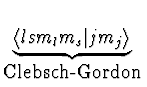 | nlsmlms | nlsmlms |
(183) |
Da in dieser Basis die Strung H2' bereits diagonal ist gilt fr die Energieverschiebung:
| (184) | |||
= 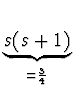
|
(185) | ||
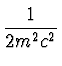 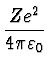
|
(186) |
Fr l=0 verschwindet die Spin-Bahn-Wechselwirkung, die Energiekorrektur ist 0.