| H = |
Hamilton-Operator | (64) | |
mit r = r1 - r2 und R = 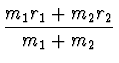 |
Substitution | (65) | |
| Zentralkoordinaten | (66) | ||
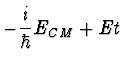 |
Separation der Anteile | (67) |
| H = |
Hamilton-Operator | (64) | |
mit r = r1 - r2 und R = 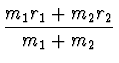 |
Substitution | (65) | |
| Zentralkoordinaten | (66) | ||
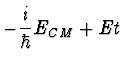 |
Separation der Anteile | (67) |
Der Schwerpunkt wird als freies Teilchen der Masse M beschrieben, der zweite Teil der Schrdingergleichung beschreibt die Relativbewegung der Teilchen im Potential V(r). Obiges gilt ohne Bercksichtiung des Spins! Fr Systeme mit Spins setzt sich das Gesamtdrehmoment aus der Kopplung der Einzelmomente zusammen.
Identische Teilchen (z. B. Elektronen)
setzen voraus, daá der Hamilton-Operator unter Teilchenvertauschung
symetrisch ist, d. h. er mit dem Teilchenvertauschungsoperator
kommutiert. Auáer fr den Fall N=2 vertauschen nicht alle N!
Permutationen miteinader, d. h. die Eigenfunktionen des
Hamilton-Operators sind nicht notwendig die Eigenfunktionen aller N!
Vertauschungsoperatoren. Es existieren aber zwei ausgezeichnete
Zustnde, fr die das der Fall ist: Der total symmetrische
und der total
antisymmetrische Zustand. Es
gilt [P,H]
![]() P ist eine konstante der Bewegung, d. h.
die Symmetrie eines Teilchensystems bleibt erhalten.
P ist eine konstante der Bewegung, d. h.
die Symmetrie eines Teilchensystems bleibt erhalten.