Betrachte: Gas mit f Freiheitsgraden aus N identischen Moleklen im
Volumen V. Koordinaten der Moleklschwerpunkte:
![]() ...
...![]() , Impulse:
, Impulse:
![]() ...
...![]() .
.
Systemenergie: E = T + UW + EI
(T: kinetische Energie, UW: Wechselwirkungsenergie, EI:
Energie intramolekularer Bewegungen). Betrachte nun den klassischen
Grenzfall UW = 0 (
![]()
![]() 0) und E
0) und E ![]() Grundzustandsenergie (=Korrespondenzprinzip).
dem Gas zugngliche Zustnde:
Grundzustandsenergie (=Korrespondenzprinzip).
dem Gas zugngliche Zustnde:
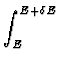 ... ...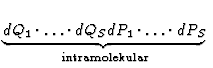
|
(31) |
Fr UW = 0
![]() d3ri = V (Energie unabhnig von
den Moleklkoordinaten). Vereinfacht man auf einatomige Molekle
fallen Intramolekulare Wechselwirkungen weg (EI = 0) E = T:
d3ri = V (Energie unabhnig von
den Moleklkoordinaten). Vereinfacht man auf einatomige Molekle
fallen Intramolekulare Wechselwirkungen weg (EI = 0) E = T:
|
2mE = |
(32) |
Wegen Energieerhaltung ist
R(E) = ![]() der Radius
einer Kugel im f = 3N-dimensionalen Raum der Impulskoordinaten.
der Radius
einer Kugel im f = 3N-dimensionalen Raum der Impulskoordinaten.
![]() (E)
(E) ![]() Volumen einer f-dimensionalen Kugelschale
mit Radien R(E) bzw.
R(E +
Volumen einer f-dimensionalen Kugelschale
mit Radien R(E) bzw.
R(E + ![]() E). mit
Vi
E). mit
Vi ![]() R(E)f = (2mE)
R(E)f = (2mE)![]() f und
Va
f und
Va ![]() (2m(E +
(2m(E + ![]() E))
E))![]() f:
f:
|
Va - Vi |
(33) |
klassisches einatomiges Gas:
|
|
(34) |
Aufhebung von Beschrnkungen bewirkt, daá die Zahl der zugnglichen Systemzustnde zunimmt oder zumindest gleich bleibt. Nimmt ihre Zahl zu, so befindet sich das System unmittelbar nach Aufheben der Beschrnkung nicht im Gleichgewicht! (s. a. H-Theorem)
Statistische Definition reversibler und irreversibler Prozesse:
Findet in einem abgeschlossenen System ein Prozess statt, bei dem das System vom Anfangs- in den Enzustand bergeht, so heiát dieser Prozess reversibel, wenn durch erneutes einfhren der Beschrnkungen das System wieder in den Anfangszusand bergeht. Ist dies nicht mglich heiát der Prozeá irreversibel.