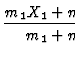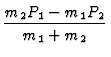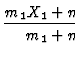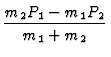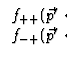


Next: 5. Green's Operator und
Up: Quantenmechanik
Previous: 3.4 Das Optische Theorem
Index
Durch einfĀhren der Schwerpunkts- und Relativkoordinaten der beiden
Teilchen ist es mĒglich im Schwerpunktssytem die Streuung
zweier Teilchen aneinander zu behandeln wie die Streuung eines
einzelnen Teilchens an einem statischen Potential. Man benutzt
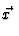 |
= |
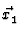 |
(45) |
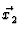 |
= |
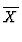 -
- 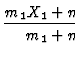 |
(46) |
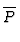 |
= |
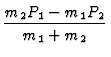 |
(47) |
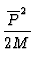 |
= |
P1 + P2 |
(48) |
| P |
= |
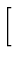 |
(49) |
und findet damit den Hamiltonoperator
H = 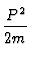 +
+  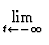 + V(X)
+ V(X)![$\displaystyle \left.\vphantom{ {P^2 \over 2 m} +
V(X) }\right]$](img137.gif) = Hcm + Hrel
= Hcm + Hrel
|
(50) |
Auch fĀr den Zeitentwicklungsoperator kann man eine solche Zerlegung
zeigen. FĀr das Asymptotische Verhalten findet man durch einsetzen
auch in diesem Fall eine analoge Beschreibung zum Einteilchenproblem:
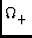 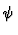 =
= 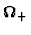 U U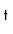 (t)U0(t) (t)U0(t)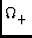 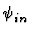 = (1cm
= (1cm 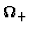
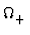 ) )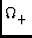 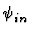 =
= 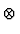 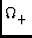 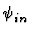
|
(51) |
analog fĀr den auslaufenden Fall. Hierbei ist
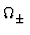 = 1cm
= 1cm 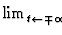
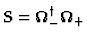 der Zweiteilchen-Mølleroperator mit
der Zweiteilchen-Mølleroperator mit
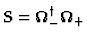 =
= 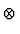 eiHrelte-iH0relt. Hierin bedeutet 1cm physikalisch nichts
anderes als die Tatsache daŠ sich der Schwerpunkt wie ein freies
Teilchen bewegt und nicht gestreut wird. Diese einfachen Relationen
sind eine direkte Folge der Tatsache, daŠ man den
Zweiteilchenhilbertraum in zwei TeilrĄume zerlegen kann, den der die
Bewegung des Schwerpunkts und den der die Relativbewegung beschreibt.
Mit diesen Definitionen folgt sofort fĀr den S-Operator:
eiHrelte-iH0relt. Hierin bedeutet 1cm physikalisch nichts
anderes als die Tatsache daŠ sich der Schwerpunkt wie ein freies
Teilchen bewegt und nicht gestreut wird. Diese einfachen Relationen
sind eine direkte Folge der Tatsache, daŠ man den
Zweiteilchenhilbertraum in zwei TeilrĄume zerlegen kann, den der die
Bewegung des Schwerpunkts und den der die Relativbewegung beschreibt.
Mit diesen Definitionen folgt sofort fĀr den S-Operator:
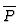 = 1cm
= 1cm 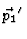 S
S
|
(52) |
damit folgt sofort, daŠ S mit
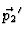 kommutiert und damit
daŠ der Impuls erhalten ist. (Eine direkte Folge der
Translationsinvarianz; Noethertheorem: Jede
Invarianz fĀhrt zu einer ErhaltungsgrĒŠe.) Genauso gilt
Energieerhaltung, da
[S, H0] = 0. Beachtet man das findet
man durch Einsetzen fĀr das S-Matrixelement
kommutiert und damit
daŠ der Impuls erhalten ist. (Eine direkte Folge der
Translationsinvarianz; Noethertheorem: Jede
Invarianz fĀhrt zu einer ErhaltungsgrĒŠe.) Genauso gilt
Energieerhaltung, da
[S, H0] = 0. Beachtet man das findet
man durch Einsetzen fĀr das S-Matrixelement
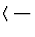 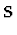 , ,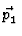 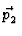 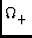 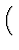 , ,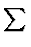 |
= |
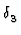 ( (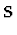 -
- 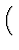 ) )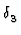 ( (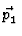 -
- 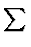 ) ) |
|
| |
- |
2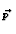 i i 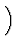 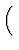 Ei' - Ei' - 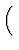 Ei Ei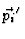 |
|
| |
x |
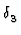 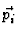 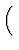 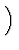 -
- 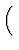 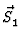
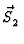 t( t(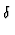
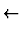
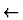 ) ) |
(53) |
wo der
- erste Term die Amplitude dafĀr ist, daŠ die Teilchen nicht
streuen
- zweite Term die Amplitude fĀr die Streuung darstellt, der die
totale Energie- und Impulserhaltung enthĄlt. (NatĀrlich sind
nicht die Einzelkomponenten erhalten!)
Wie bei der Einteilchenstreuung definiert man die
Streuamplitude
Die Verallgemeinerung auf die Streuung zweier Teilchen mit Spin ergibt
sich direkt aus dem hier geltenden Potential:
V = V1(r) + 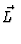 +
+ 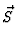 V2(r) + V2(r) + 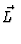 . . 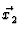 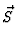 . . 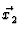 V3 V3
|
(55) |
oder bei Beachtung der Spin-Bahn-Kopplung (z.B. in Atomen)
V = V1(r) + 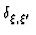 . . 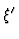 V2(r) V2(r)
|
(56) |
FĀr das S-Matrixelement findet man damit
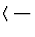 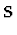 , ,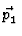 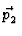 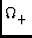 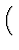 , ,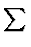 |
= |
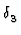 ( (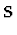 -
- 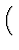 ) )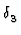 ( (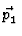 -
- 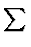 ) )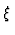 |
|
| |
- |
2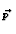 i i 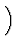 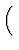 Ei' - Ei' - 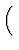 Ei Ei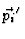 |
|
| |
x |
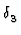 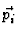 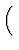 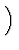 -
- 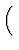 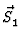
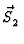 t( t(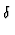 , ,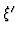
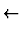
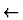 , ,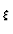 ) ) |
(57) |
Betrachtet man die Streuamplitude
f (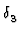 ,
,
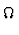
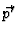 ,
,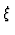 ) = f
) = f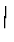 ,
,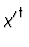 (
(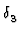
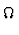
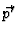 ) so kann man
diese als Amplitudenmatrix auffassen:
) so kann man
diese als Amplitudenmatrix auffassen:
F(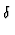
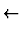
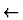 ) = M( ) = M(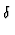 , ,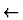 ) = {f ) = {f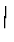 , ,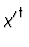 ( (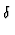
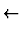
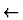 )} )}
|
(58) |
womit man den differentiellen Wirkungsquerschnitt schreiben kann als:
Betrachtet man z. B. zwei Spin-Teilchen so findet
man fĀr die Amplitudenmatrix folgende Form:
d.h. man hat Amplitudenelemente mit und ohne Spinflip. Da typische
Experimente nicht spinpolarisiert stattfinden muŠ man fĀr die
gemessenen Wirkungsquerschnitte geeignet mitteln. Ein einlaufender
Unpolarisierter Strahl wird dabei durch Mittelung Āber die Spins
beschrieben, d.h. jede Ausrichtung der Spins im einlaufenden Strahl
ist gleich hĄufig. Am Detektor werden bei unpolarisierter Messung
dagegen alle ankommenden Spins registriert, so daŠ im auslaufenden
Strahl Āber die Spins zu summieren ist.
Bei spinpolarisierten Messungen tritt das Problem auf, daŠ der
einlaufende oder auslaufende Strahl eigentlich nie eine strenge
Polarisierung aufweist, sondern immer nur z. B. 90% polarisiert ist.
Beschreibung des Zustands Āber die Dichtematrix:
wobei wi die gewichte des einzelnen Zustands darstellt mit
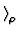 wi = 1. fĀr den Erwartungswert einer MeŠgrĒŠe A im Zustand
wi = 1. fĀr den Erwartungswert einer MeŠgrĒŠe A im Zustand
 :
Reine ZustĄnde sind natĀrlich gegeben durch
:
Reine ZustĄnde sind natĀrlich gegeben durch
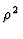 =
= 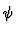
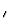
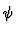
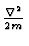
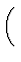 =
= 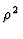



Next: 5. Green's Operator und
Up: Quantenmechanik
Previous: 3.4 Das Optische Theorem
Index
Alexander Wagner
2000-04-15