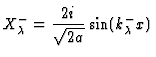 |
(9) | ||
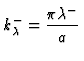 |
(10) | ||
| (11) | |||
| (12) | |||
| p2 = 2 m E | (13) |
Voraussetzung: Unabhngige, nicht miteinander wechselwirkende Teilchen. D. h. Nukleon bewegt sich in einem mittleren Potential, die Nukleon-Nukleon-Wechselwirkung wird vernachlssigt.
Einfaches Modell: nichtwechselwirkende Spin-Teilchen in einem 3D-Potentialkasten mit unendlich hohen Wnden bei r=R. Lsung der Schrdingergleichung liefert
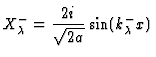 |
(9) | ||
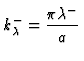 |
(10) | ||
| (11) | |||
| (12) | |||
| p2 = 2 m E | (13) |
Betrachte nun im Phasenraum die Anzahl der Energieeigenwerte in einer
Kugel mit Radius r, d.h. das Integral der Zustandsdichte.
Die Zahl der Zustnde im Volumen ![]() ist quantenmechanisch
gegeben durch:
ist quantenmechanisch
gegeben durch:
| (14) |
Mit
![]() ergibt sich daraus die
Zustandsdichte1:
ergibt sich daraus die
Zustandsdichte1:
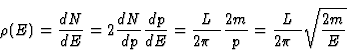 |
(15) |
Fr die Zahl der Zustnde pro Impulsintervall gilt wenn ![]() :
:
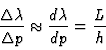 |
(16) |
Dies gilt bisher in einer Dimension. In 3D gilt fr das Zellvolumen
h3 und das Volumen des Phasenraums
![]() .
Damit folgt:
.
Damit folgt:
| (17) | |||
| (18) |
Fr die Zustnde in der Kugelschale ergibt sich damit durch Integration ber d3p:
| (19) |
wo
![]() das Kernvolumen ist. Hieraus folgt die
Fermienergie fr jede Nukleonensorte durch Einsetzen von
das Kernvolumen ist. Hieraus folgt die
Fermienergie fr jede Nukleonensorte durch Einsetzen von
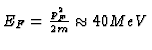 :
:
| (20) |
Bisher: Fr Protonen wird die Coulomb-Kraft nicht bercksichtigt.
![]() Zwei unabhngige Fermigase im Kern: Protonen und
Neutronen. Fr die Protonen muá noch das Coulomb-Potential
bercksichtigt werden
Zwei unabhngige Fermigase im Kern: Protonen und
Neutronen. Fr die Protonen muá noch das Coulomb-Potential
bercksichtigt werden ![]() Erniedigung der Bindungsenergie.
Erniedigung der Bindungsenergie.
Fr stabile Kerne muá die Fermienergie fr Protonen und Neutronen etwa gleich hoch liegen, da sich sonst Neutronen in Protonen umwandeln wrden und umgekehrt, wenn unterhalb einer Fermikante ein unbesetzes Niveau vorlge.