next up previous contents
Next: 9. Quantenfeldtheorie Up: 8.2 Relativitätstheorie Previous: 8.2.1.0.5 Gemischter Tensor   Inhalt

8.2.2 Vektorraumeigenschaften

Linienelement

ds2 = (dx0)2 - (dx1)2 - (dx2)2 - (dx3)2 = g$\scriptstyle \alpha$$\scriptstyle \beta$dx$\scriptstyle \alpha$dx$\scriptstyle \beta$ (8.8)

Mit dem metrischen Tensor g$\scriptstyle \alpha$$\scriptstyle \beta$

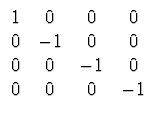
g$\scriptstyle \alpha$$\scriptstyle \beta$ = $\displaystyle \left(\vphantom{ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \\ \end{array}}\right.$$\displaystyle \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \\ \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \\ \end{array}}\right)$ (8.9)

Es gilt:


  g$\scriptstyle \alpha$$\scriptstyle \beta$ = g$\scriptstyle \alpha$$\scriptstyle \beta$   (8.10)
  g$\scriptstyle \alpha$$\scriptstyle \beta$g$\scriptstyle \alpha$$\scriptstyle \beta$ = $\displaystyle \delta^{.\beta}_{\alpha .}$   (8.11)
  x$\scriptstyle \alpha$ = g$\scriptstyle \alpha$$\scriptstyle \beta$x$\scriptstyle \beta$   (8.12)
  x$\scriptstyle \alpha$ = g$\scriptstyle \alpha$$\scriptstyle \beta$x$\scriptstyle \beta$   (8.13)
  A$\scriptstyle \alpha$ = (A0, A1, A2, A3) $\displaystyle \Rightarrow$ A$\scriptstyle \alpha$ = (A0, - A1, - A2, - A3)   (8.14)

Skalarprodukt

A . B = B$\scriptstyle \alpha$A$\scriptstyle \alpha$ = B0A0 - $\displaystyle \vec{A}\,$ . $\displaystyle \vec{B}\,$ (8.15)


Alexander Wagner
2000-04-14