| Wellenfunktion | (69) | ||
| Ek = |
Energie | (70) |
Bei einer kleinen Strung kann man H die Wellenfunktion und die Energieeigenwerte entwickeln:
| Wellenfunktion | (69) | ||
| Ek = |
Energie | (70) |
wo n die Ordnung der Strung beschreibt. Damit schreibt sich die Schrdingergleichung:
|
(H0 + |
(71) |
Sortiert nach gleicher Ordnung in ![]() folgt:
folgt:
| H0 |
ungestrt | (72) | |
| H0 |
erste Ordnung | (73) | |
| H0 |
2. Ordnung | (74) | |
| ... |
Die Energiekorrektur erhlt man durch
Multiplikation der Gleichungen mit ![]() von links und
Integration ber den gesamten Raum (=
Projektion auf die neue Basis!). Man findet
von links und
Integration ber den gesamten Raum (=
Projektion auf die neue Basis!). Man findet
| Ek(1) = |
1. Ordnung | (75) | |
| Ek(2) = |
2. Ordnung | (76) |
Bestimmung der Lsung nach Rayleigh-Schrdinger:
|
(H0 - Ek) |
(77) |
|
al(1)(El - Ek) + |
(78) |
al(1) = 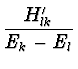 |
(79) |
Damit folgen die endgltigen Ergebnisse:
|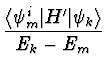 | | |
Wellenfunktion | (80) | |
| Ek(1) = |
Energiekorrektur in 1. Ordnung | (81) | |
Ek(2) = 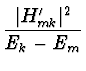 |
Energiekorrektur 2. Ordnung | (82) |
Fr die Wellenfunktion taucht noch der Index i auf, da es sein kann, daá das ein anderes Energienieveau als das gerade betrachtete entartet sein knnte.
Die Energiekorrektur in erster Ordnung ist im nichtentarteten Fall gleich dem Mittelwert der Strung in den ungestrten Zustnden!