4.1 Welle-Teilchen-Dualismus

$\displaystyle \nu$ = $\displaystyle {E \over h}$	Frequenz eines Teilchens	(25)
$\displaystyle \lambda$ = $\displaystyle {h \over p}$	de-Broglie-Wellenl„nge	(26)
$\displaystyle \lambda$ = $\displaystyle {h \over m v}$	Nichtrelativistisch	(27)
$\displaystyle \Rightarrow$ n $\displaystyle \lambda$ = 2 $\displaystyle \pi$ r	Bedinung fr stabile Bohr-Bahn	(28)
$\displaystyle \Rightarrow$ L = h $\displaystyle \hbar$	entspricht Bohrschem Postulat!	(29)

1927: Experimente von Davisson und Germer, die den Wellencharakter des Elektrons zeigen (Beugung von Elektronen an Kristallgittern).

$\displaystyle \omega$ = 2 $\displaystyle \pi$ $\displaystyle \nu$ = $\displaystyle {\hbar k^2 \over 2 m}$	k = $\displaystyle {2 \pi \over \lambda}$	$\displaystyle \hbar$ = $\displaystyle {h \over 2\pi}$	(30)
$\displaystyle \Rightarrow$ E = $\displaystyle \hbar$ $\displaystyle \omega$	p = $\displaystyle \hbar$ k	Symmetrische Form	(31)

$\displaystyle \Psi$ ( $\displaystyle \vec{r}\,$ , t) = Aexp(i( $\displaystyle \vec{k}\,$ ^. $\displaystyle \vec{r}\,$ - $\displaystyle \omega$ t))	Wellenfunktion	(33)
$\displaystyle \vec{p}\,$ = $\displaystyle \hbar$ $\displaystyle \vec{k}\,$	Wellenvektor und Impuls	(34)
\| $\displaystyle \vec{k}\,$ \| = k = $\displaystyle {\vert\vec{p}\vert \over \hbar}$ = $\displaystyle {2 \pi \over \lambda}$	Betrag des Wellenvektors	(35)
$\displaystyle \omega$ = $\displaystyle {E \over \hbar}$ = $\displaystyle {\hbar k^2 \over 2 m}$	Frequenz	(36)
- i $\displaystyle \hbar$ $\displaystyle \nabla$ $\displaystyle \Psi$ = E $\displaystyle \Psi$	Wellenfunktion	(37)
E_op = i $\displaystyle \hbar$ $\displaystyle {\partial \over \partial t}$	Energieoperator	(38)
p_op = - i $\displaystyle \hbar$ $\displaystyle \nabla$	Impulsoperator	(39)

Lokalisierte Teilchen werden durch šberlagerung von Wellen zu einem Wellenpacket beschrieben:

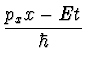
$\displaystyle \Psi$ (x, t) = $\displaystyle \underbrace{\sqrt{1 \over 2 \pi \hbar}}_{Normierung}^{}\,$ $\displaystyle \int_{-\infty}^{\infty}$ exp $\displaystyle {{p_x x - E t} \over \hbar}$ $\displaystyle \phi$ (p_x)dp_x

Daraus ergibt sich, wenn man $\psi$ (x) = $\Psi$ (x, 0) schreibt, daá die Funktionen $\psi$ (x) und $\phi$ (x) auseinader durch Fouriertransformation entstehen. (Dartellung im Orts- ( $\Psi$ ) und Impulsraum ( $\Phi$ )!). Auch die Zeitabh„ngigen Funktionen gehen so ineinader ber. Daraus folgt die Heisenbergsche Unsch„rferelation, eine generelle Eigenschaft der Fouriertransformation:

$\displaystyle \Delta$ x $\displaystyle \Delta$ p $\displaystyle \geq$ $\displaystyle \hbar$		Ort und Impuls	(40)
$\displaystyle \Delta$ E $\displaystyle \Delta$ t $\displaystyle \geq$ $\displaystyle \hbar$		Energie und Zeit	(41)